Hace ya algunos años, cuando yo molaba como me dicen algunos, que estudié el Teorema de Rolle. Este teorema dice lo siguiente:
Si se cumplen estas tres condiciones:
ƒ es una función continua definida en un intervalo cerrado [a, b] y
ƒ es derivable sobre el intervalo abierto (a, b)
ƒ(a) = ƒ(b)
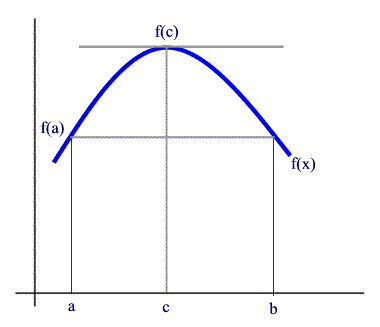 Podemos afirmar que existe por lo menos un número c perteneciente al intervalo (a, b) de tal manera que ƒ'(c) = 0
Podemos afirmar que existe por lo menos un número c perteneciente al intervalo (a, b) de tal manera que ƒ'(c) = 0
Para los profanos en matemáticas esto significa que si una curva sale de un punto determinado y en otro punto llega a la misma altura, podemos afirmar que existe al menos un punto donde su tangente sea paralela al eje de abcisas, es decir, sea horizontal.
No me voy a detener en su demostración, pero, alguno de vosotros se preguntará… ¿Que tiene que ver esto con la economía?
El economista Arthur Laffer representó en la famosa curva que lleva también su nombre la relación que existe entre los ingresos provenientes de los impuestos de un estado y el tipo impositivo de estos. Si nos fijamos en la gráfica anterior y representamos en el eje de abcisas (el horizontal) el tipo impositivo y en el eje de ordenadas los ingresos, podemos observar lo siguiente:
A tipo impositivo 0 el estado recaudaría 0 y a tipo impositivo 100, el estado recaudaría igualmente 0, puesto que nadie demandaría ningun tipo de servicio. Por lo tanto, ya tenemos una curva que cumple con los requisitos arriba mencionados. Si aplicamos el Teorema de Rolle veremos que existe un punto c donde ƒ'(c)=0.
¿Cual sería este punto? ¿Que tiene de bueno este punto? ¿Como podemos aplicarlo en nuestra economía? Si habéis entendido el teorema, observareis que este punto es aquel donde la recaudación del estado (que no del tipo impositivo) es mayor, es decir, podríamos ajustar el tipo impositivo para que la recaudación del estado fuera máxima. A partir de este punto, tanto si subimos el tipo impositivo como si lo bajamos, los ingresos del estado serían inferiores.
Milton Friedman afirmó que «If a tax cut increases government revenues, you haven’t cut taxes enough» (Si una reducción de impuestos aumenta los ingresos del gobierno, es que no se han reducido los impuestos lo suficiente).
En la economía española está pasando justamente lo contrario, es decir, esta subiendo el tipo impositivo y sin embargo está bajando la recaudación. Si nos fijamos nuevamente en la curva, podremos observar que nos debemos de encontrar en la segunda mitad de ella y que por mucho que los subamos, los ingresos cada vez van a ser inferiores y lo que debemos hacer, o mejor dicho, lo que tienen que hacer nuestros dirigentes es bajar los tipos impositivos.
Una vez mas, con nuestras amigas las matemáticas, podemos explicar y demostrar todo.
3 Responses
Y estas cosas ya las sabe don Mariano?
Parece ser que vive en un mundo o en una dimensión distinta a la nuestra.
Si éste fuera el caso, volvemos a repetir, debería haber algún punto entre el 0% y el 100% donde resida un tipo impositivo ideal que maximice la recaudación. Las representaciones gráficas de la curva a menudo reflejan ese punto en torno al 50%, pero eso es una idealización, no un hecho. De la misma manera, la curva a menudo se presenta como una parábola, pero no tiene por qué darse necesariamente el caso.