 La informática está muy ligada a las matemáticas. Cada vez que desarrollo software tengo que recurrir a ingeniosos procedimientos creados por matemáticos muchos años atrás.
La informática está muy ligada a las matemáticas. Cada vez que desarrollo software tengo que recurrir a ingeniosos procedimientos creados por matemáticos muchos años atrás.
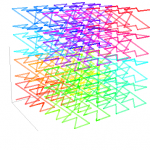
Esta vez tenía que construir una estructura que definiera puntos en una matriz multidimensional y por supuesto indexar esos datos por un solo valor unidimensional. Lo primero que me ha venido a la cabeza ha sido utilizar la famosa Curva de Hilbert que me permite recubrir todo el plano.
Pero calcular esta curva teniendo en cuenta que es una curva fractal, es muy costosa computacionalmente hablando y no me puedo permitir ese lujo puesto que necesito consumir los mínimos recursos posibles.
Por suerte, en 1966 G.M. Morton cuando trabajaba para IBM Canadá desarrolló un procedimiento para para indexar puntos denifidos en Rn dando como resultado un valor en R y lo mas importante de todo es que mantiene la localidad de las celdas.
Este valor es calculado entrelazando la representación binaria de cada una de las coordenadas de un determinado punto. Por ejemplo, si tenemos un punto A(7,4,5) calculamos su Número Morton o Z-valor de la siguiente manera:
A (7, 4, 5) = (0111, 0100, 0101)
Y ahora entrelazamos los valores para calcular el valor.
A’=(000 111 100 101)
Algo tan simple como entrelazar los dígitos que componen las coordenadas de un punto nos ahorra muchos cálculos porque nos permite operar rápidamente sobre un punto. Podemos calcular rápidamente distancias, colisiones entre puntos asi como obtener fácilmente los vecinos de un punto determinado.
Pero aquí no acaba todo, en álgebra lineal, el algoritmo de Strassen utilizado en la multiplicación de matrices se apoya en ir intercambiando la posición de las celdas.
No responses yet